出版論文の中から選んだものを紹介していますが,気儘に更新しているため,情報がやや古くなりがちです.最新かつ完全な論文リストは researchmap を御覧ください.
二次元多谷半導体系におけるポリ励起子
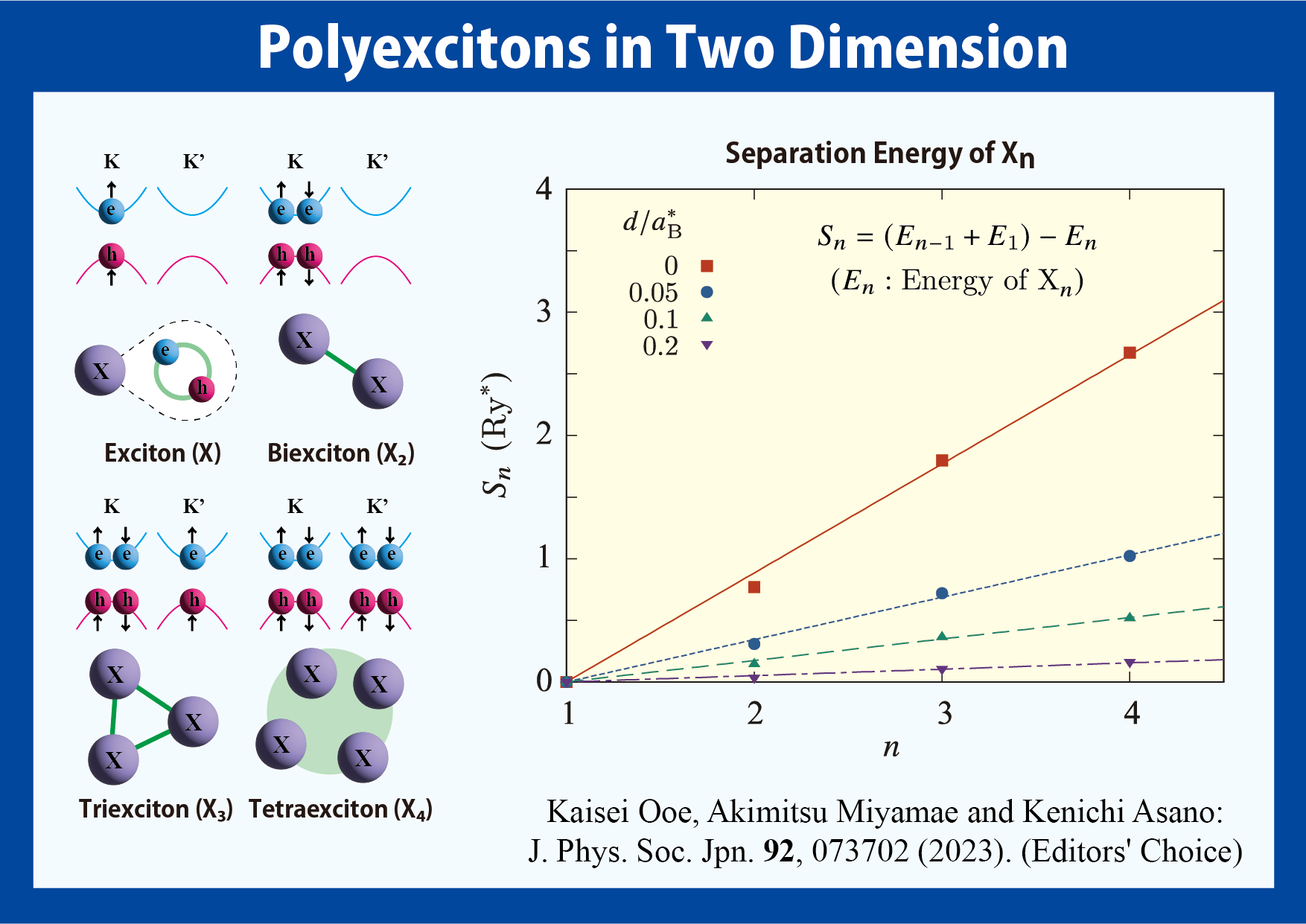 ポリ励起子は,複数個の励起子(電子と正孔の束縛状態)が結合した多量体です.一般の半導体では,励起子の二量体(励起子分子)は形成されますが,三量体以上のポリ励起子は形成されません.これは,電子(正孔)がスピン自由度以外に内部自由度を持たないので、パウリ排他律によって、二個以上の電子(正孔)が同じ位置を占めることができないためです.
ポリ励起子は,複数個の励起子(電子と正孔の束縛状態)が結合した多量体です.一般の半導体では,励起子の二量体(励起子分子)は形成されますが,三量体以上のポリ励起子は形成されません.これは,電子(正孔)がスピン自由度以外に内部自由度を持たないので、パウリ排他律によって、二個以上の電子(正孔)が同じ位置を占めることができないためです.
本研究では,二重二層グラフェンのタイプII構造を念頭において,電子と正孔がそれぞれ異なる二次元面に閉じ込められ,スピンだけでなくバンドの多谷構造に由来する四つの内部自由度を持つ系を考察して,パウリ原理の制限緩和により,励起子の三量体および四量体が形成されることを,量子拡散モンテカルロ法を用いて数値的に厳密に示しました.
その結果,励起子 n 量体の分離エネルギー( n 量体を n-1 量体と励起子に分離するのに要するエネルギー)が,僅かなずれを除けば n-1 に比例していることがわかりました. この結果は,あらゆる励起子の対の間にほぼ等価な化学結合が形成されていることを示唆しています.
その結果,励起子 n 量体の分離エネルギー( n 量体を n-1 量体と励起子に分離するのに要するエネルギー)が,僅かなずれを除けば n-1 に比例していることがわかりました. この結果は,あらゆる励起子の対の間にほぼ等価な化学結合が形成されていることを示唆しています.
- Kaisei Ooe, Akimitsu Miyamae and Kenichi Asano: J. Phys. Soc. Jpn. 92, 073702 (2023). (Editors' Choice)
籠目格子 Hubbard モデルにおける金属絶縁体転移
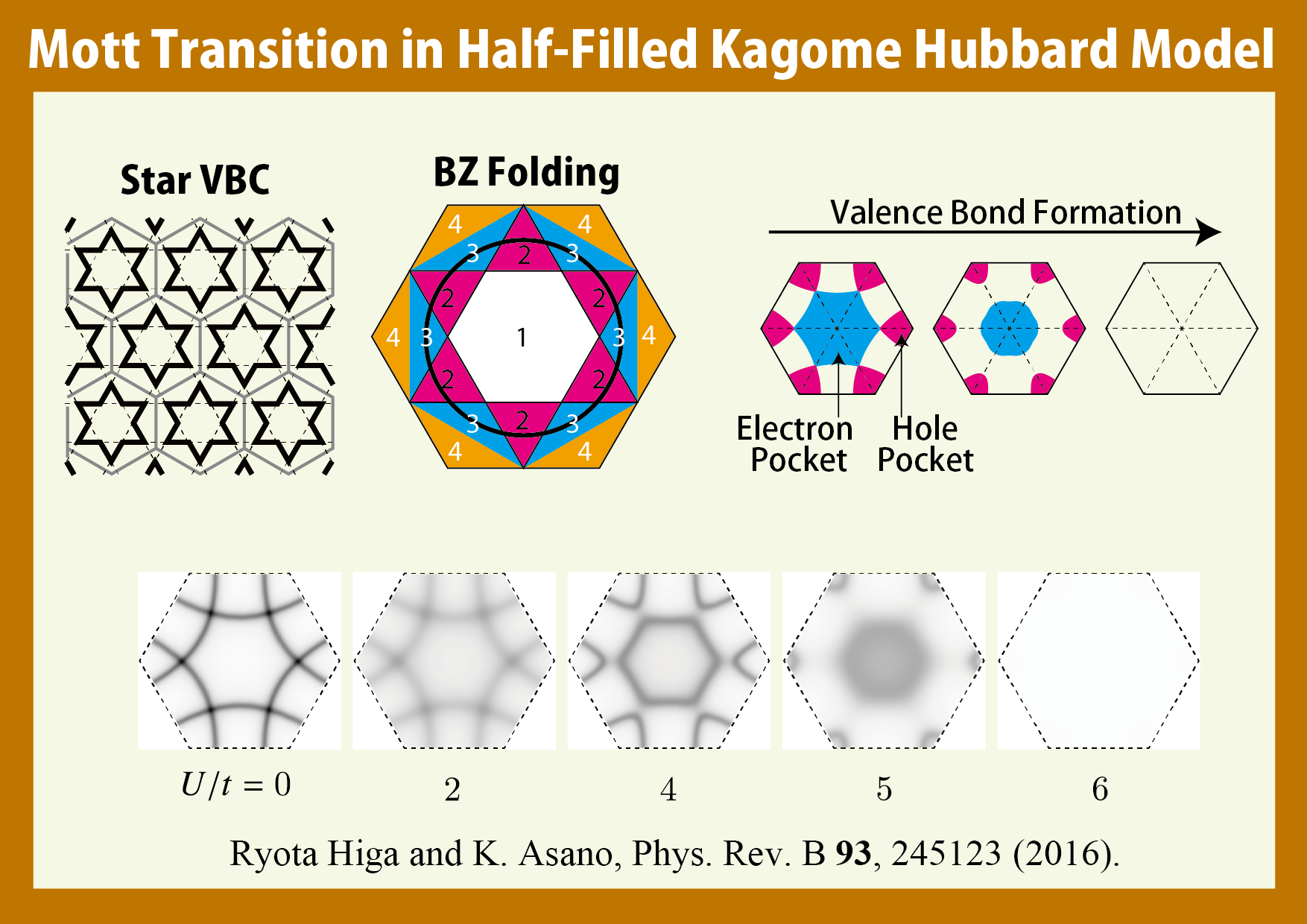 ハーフフィリングの籠目格子 Hubbard モデルで,相互作用起因の金属絶縁体転移を調べました.籠目格子では強い磁気的フラストレーションが生じます.実際,この系の強結合極限に当たる反強磁性
Heisenberg モデルの基底状態は,120°Néel 秩序のような単純な磁気秩序構造を示しません.そのため過去の研究では,基底状態に何の磁気秩序も現れず,Slater
機構(磁気秩序発現による新たなバンド分裂)が抑制され,Brinkman-Rice 機構(フェルミ準位上にある準粒子の質量の発散)によって,金属絶縁体転移が起こると考えられていました.
ハーフフィリングの籠目格子 Hubbard モデルで,相互作用起因の金属絶縁体転移を調べました.籠目格子では強い磁気的フラストレーションが生じます.実際,この系の強結合極限に当たる反強磁性
Heisenberg モデルの基底状態は,120°Néel 秩序のような単純な磁気秩序構造を示しません.そのため過去の研究では,基底状態に何の磁気秩序も現れず,Slater
機構(磁気秩序発現による新たなバンド分裂)が抑制され,Brinkman-Rice 機構(フェルミ準位上にある準粒子の質量の発散)によって,金属絶縁体転移が起こると考えられていました.
我々は,磁性秩序発現の可能性まで考察できるクラスター変分法を用いて,この系を考察しました.予想通り,あらゆる相互作用領域で,基底状態が120°Néel
秩序を示さないことが確認されました.しかしその一方で,絶対零度の金属絶縁体転移が,これまで信じられていたような Brinkman-Rice 機構ではなく,valence-bond(VB)
が結晶化した非自明な秩序を形成することによる Slater
機構で説明されることが分かりました.つまり,相互作用起因のバンド分裂により,セミメタルから絶縁体への転移が起きる訳です.実空間描像で見れば,VB
(一重項を組んだサイト対)が形成され,このサイト対に電子が局在するために金属絶縁体転移が引き起こされていることになります.
数値計算で用いているクラスターのサイズに限界があるため,実際の系ではより複雑な構造の VB 結晶や結晶が融解したスピン液体が実現する可能性が残ります.しかしそれでも,サイト対に電子が局在して金属絶縁体転移が起きるという描像自体は正しいと考えています.
数値計算で用いているクラスターのサイズに限界があるため,実際の系ではより複雑な構造の VB 結晶や結晶が融解したスピン液体が実現する可能性が残ります.しかしそれでも,サイト対に電子が局在して金属絶縁体転移が起きるという描像自体は正しいと考えています.
- Ryota Higa and Kenichi Asano: Physical Review B 93, 245123 (2016).
電子正孔系のグローバル相図
 半導体を強く光励起すると,多数の電子が価電子バンドから伝導バンドへ励起されます.このとき,伝導バンドに励起された電子(以降は単に電子と呼ぶ)は負電荷を持ったフェルミオン,価電子バンドに残された電子の空席(正孔)は正電荷を持ったフェルミオンとして振る舞い,電子同士および正孔同士にクーロン斥力,電子正孔間にクーロン引力が働きます.一般に,励起された電子と正孔が光を放出して対消滅するのに要する時間スケールはバンド内で起こる格子振動による散乱やキャリア間散乱の時間スケールよりも長いので,両者の中間の時間スケールで,電子と正孔が多数共存したまま擬似的な熱平衡状態に達した状況を実現できます.
半導体を強く光励起すると,多数の電子が価電子バンドから伝導バンドへ励起されます.このとき,伝導バンドに励起された電子(以降は単に電子と呼ぶ)は負電荷を持ったフェルミオン,価電子バンドに残された電子の空席(正孔)は正電荷を持ったフェルミオンとして振る舞い,電子同士および正孔同士にクーロン斥力,電子正孔間にクーロン引力が働きます.一般に,励起された電子と正孔が光を放出して対消滅するのに要する時間スケールはバンド内で起こる格子振動による散乱やキャリア間散乱の時間スケールよりも長いので,両者の中間の時間スケールで,電子と正孔が多数共存したまま擬似的な熱平衡状態に達した状況を実現できます.
このような擬似的熱平衡状態下の電子正孔系は,物質系を究極まで簡約したモデルとみなせます.なぜならすべての物質は,負電荷を持つ電子と,正電荷を持つ原子核の集合体だからです.実際に電子正孔系を研究すると,Mott
転移や BCS-BEC
クロスオーバーをはじめとして,現代物性論の中核を成すほとんどのキーワードに出会うことができます.電子正孔系はまさに「物質科学の縮図」なのです.電子正孔系の研究は応用面から見ても重要です.例えば半導体レーザーは電子正孔プラズマが反転分布を形成して光学利得を生じる機構を利用します.
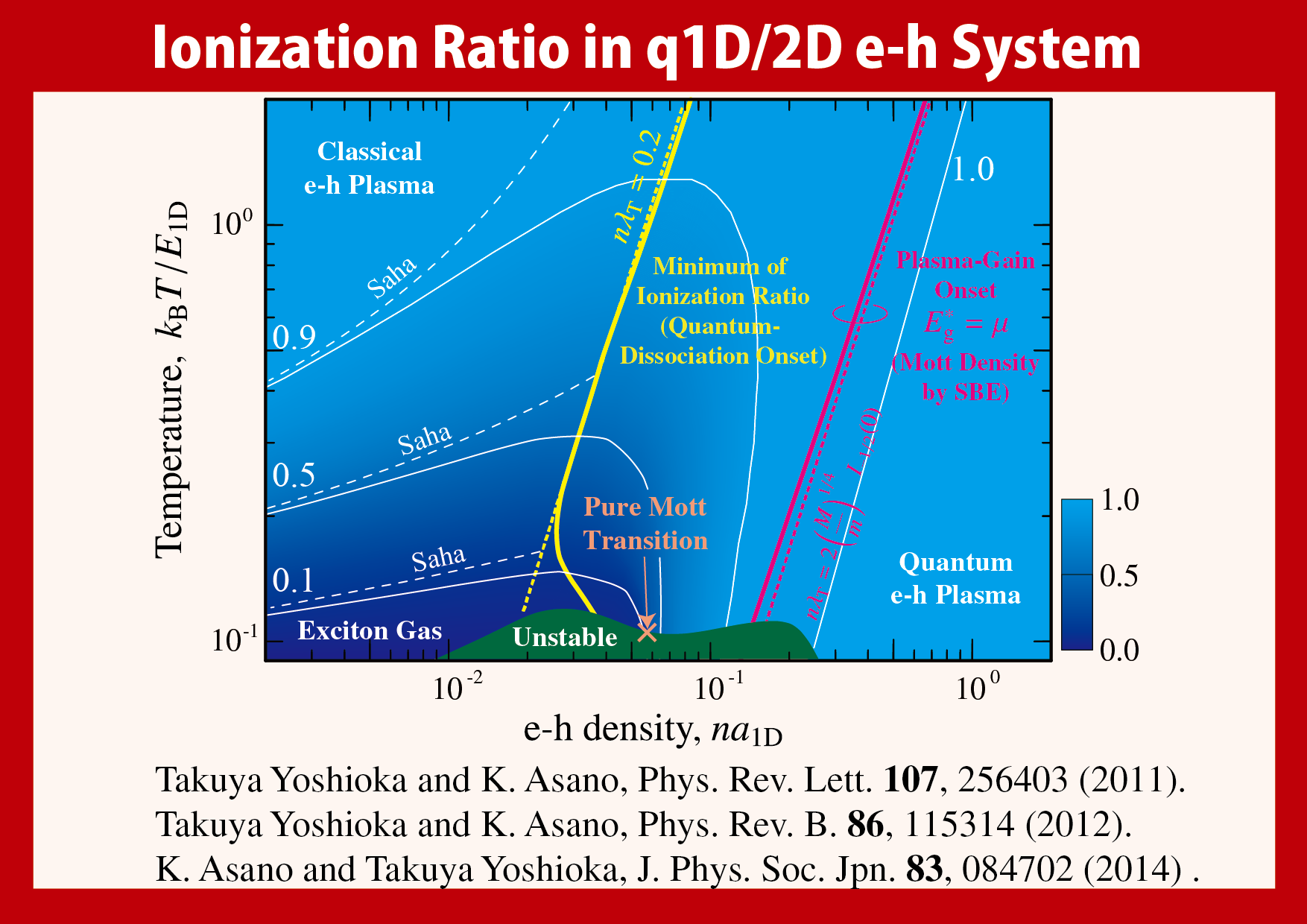
しかしこれまで,電子正孔系の相図を広い密度・温度領域に渡って,統一的に調べることができる理論手法は確立していませんでした.我々はこれを可能にする新たな理論手法(遮蔽された自己無撞着 T 行列近似)を開発し,実際にそれを強く光励起された量子細線系の問題に適用して,大域的な相図を描くことに成功しました.さらに,光の吸収利得スペクトルを計算し,現象論的なパラメーターを導入することなく半定量的に実験データを再現することができました.
しかしこれまで,電子正孔系の相図を広い密度・温度領域に渡って,統一的に調べることができる理論手法は確立していませんでした.我々はこれを可能にする新たな理論手法(遮蔽された自己無撞着 T 行列近似)を開発し,実際にそれを強く光励起された量子細線系の問題に適用して,大域的な相図を描くことに成功しました.さらに,光の吸収利得スペクトルを計算し,現象論的なパラメーターを導入することなく半定量的に実験データを再現することができました.
- Takuya Yoshioka and Kenichi Asano: Physical Review Letters 107, 256403 (2011).
- Takuya Yoshioka and Kenichi Asano: Physical Review B 86, 115314 (2012).
- Kenichi Asano and Takuya Yoshioka: Journal of the Physical Society of Japan 83, 084702 (2014).
半導体カーボンナノチューブ上の荷電励起子と励起子分子
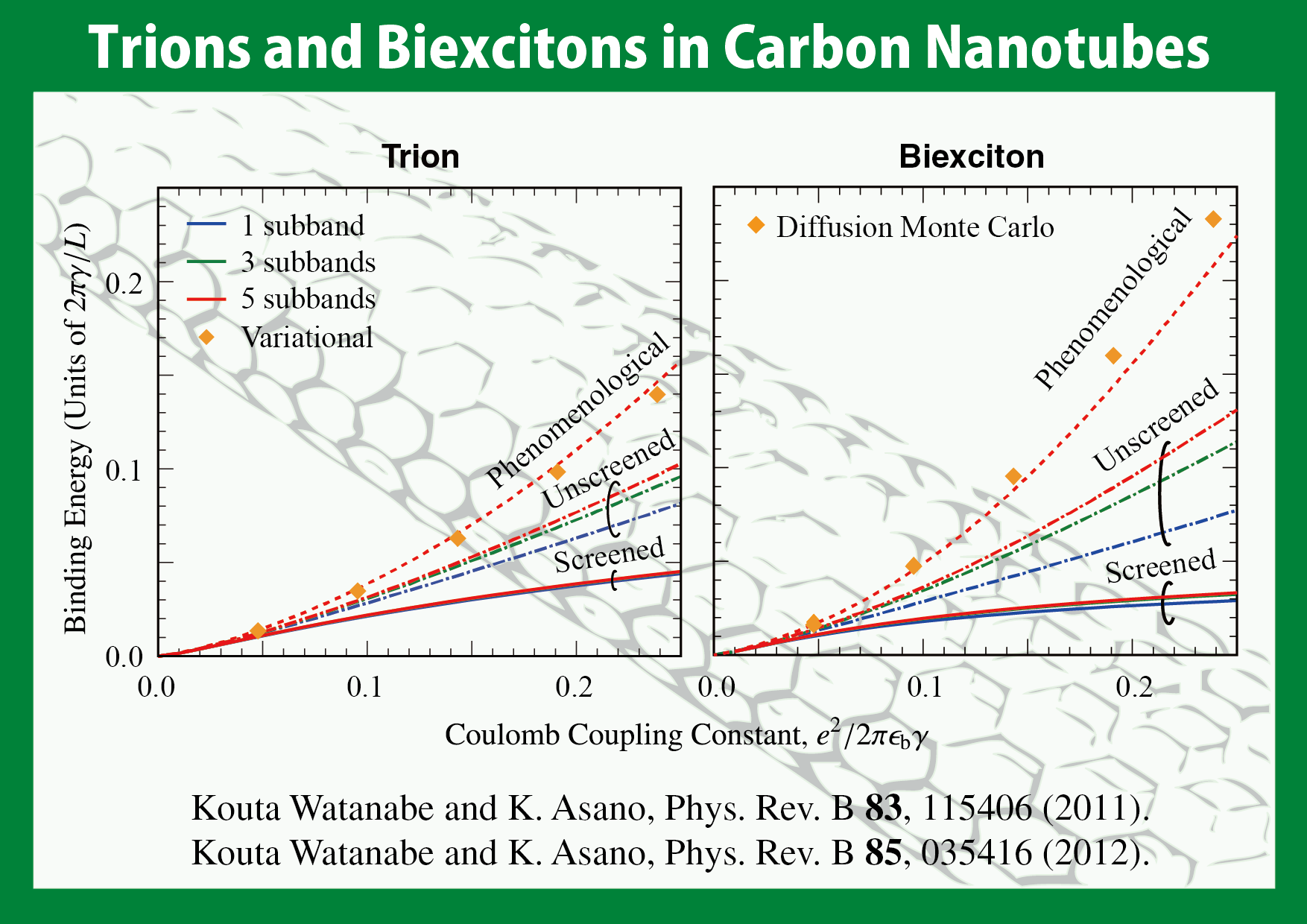 低次元系では励起子(電子と正孔の束縛状態)がバルク(三次元)系に比べて非常に大きな束縛エネルギーを持つことが知られています.一層のグラファイト(グラフェン)を,一定のルールに従って丸めて筒状にすることにより,理想的な一次元半導体系(半導体カーボンナノチューブ)を作ることができますが,これに光を当てて作られる励起子も,例に漏れず非常に大きな束縛エネルギーを持ちます.このことから,荷電励起子(電子二個と正孔,あるいは電子一個と正孔二個の束縛状態)や励起子分子(電子二個と正孔二個の束縛状態)も大きな束縛エネルギーを持つことが予想されていました.
低次元系では励起子(電子と正孔の束縛状態)がバルク(三次元)系に比べて非常に大きな束縛エネルギーを持つことが知られています.一層のグラファイト(グラフェン)を,一定のルールに従って丸めて筒状にすることにより,理想的な一次元半導体系(半導体カーボンナノチューブ)を作ることができますが,これに光を当てて作られる励起子も,例に漏れず非常に大きな束縛エネルギーを持ちます.このことから,荷電励起子(電子二個と正孔,あるいは電子一個と正孔二個の束縛状態)や励起子分子(電子二個と正孔二個の束縛状態)も大きな束縛エネルギーを持つことが予想されていました.
ただし,先行研究で行われた計算では,バンドの非放物線性,構造因子,遮蔽効果,自己エネルギー補正といったカーボンナノチューブの特性がすべて無視されていたため,他の一次元半導体系との違いがよくわからないままでした.我々はこれらの効果をすべて取り込んだ計算を行ないました.その結果,主にバンド間遮蔽効果と構造因子の効果により,荷電励起子や励起子の束縛エネルギーが,先行研究で予想されていた値の半分以下にまで抑制されることが分かりました.
この抑制効果は荷電励起子よりも励起子分子に対して強く働くため,荷電励起子の方が励起子分子よりも大きな束縛エネルギーを持ちます.通常の半導体系では,励起子分子が荷電励起子よりも大きな束縛エネルギーを持つのが普通で,カーボンナノチューブに対する先行研究の計算結果もそうなっていました.我々が見出した束縛エネルギーの逆転は,カーボンナノチューブの特性を考慮してはじめて理解できる物理です.最近,この逆転を観測したという報告もあり,今後の実験による検証が期待されます.
この抑制効果は荷電励起子よりも励起子分子に対して強く働くため,荷電励起子の方が励起子分子よりも大きな束縛エネルギーを持ちます.通常の半導体系では,励起子分子が荷電励起子よりも大きな束縛エネルギーを持つのが普通で,カーボンナノチューブに対する先行研究の計算結果もそうなっていました.我々が見出した束縛エネルギーの逆転は,カーボンナノチューブの特性を考慮してはじめて理解できる物理です.最近,この逆転を観測したという報告もあり,今後の実験による検証が期待されます.
- Kouta Watanabe and Kenichi Asano: Physical Review B 83, 115406 (2011).
- Kouta Watanabe and Kenichi Asano: Physical Review B 85, 035416 (2012).
Dirac 電子系の設計
 最近二次元格子系で次々と Dirac 電子系(エネルギーバンドが Dirac
コーン型の構造を持つ電子系)が見つかっています.一番の代表格はグラフェンですが,例えば有機導体系のα-ET2I3 や鉄ヒ素系超伝導体 LaOFeAs
でもエネルギーバンドに Dirac コーンが現れます.特にα-ET2I3 で見つかった Dirac 点(Dirac
コーンの頂点)は,Brillouin ゾーン内部の一般点(特別な対称性を持たない k
点)に位置しており,Dirac 点が偶然縮退として現れていることを示しています.
最近二次元格子系で次々と Dirac 電子系(エネルギーバンドが Dirac
コーン型の構造を持つ電子系)が見つかっています.一番の代表格はグラフェンですが,例えば有機導体系のα-ET2I3 や鉄ヒ素系超伝導体 LaOFeAs
でもエネルギーバンドに Dirac コーンが現れます.特にα-ET2I3 で見つかった Dirac 点(Dirac
コーンの頂点)は,Brillouin ゾーン内部の一般点(特別な対称性を持たない k
点)に位置しており,Dirac 点が偶然縮退として現れていることを示しています.
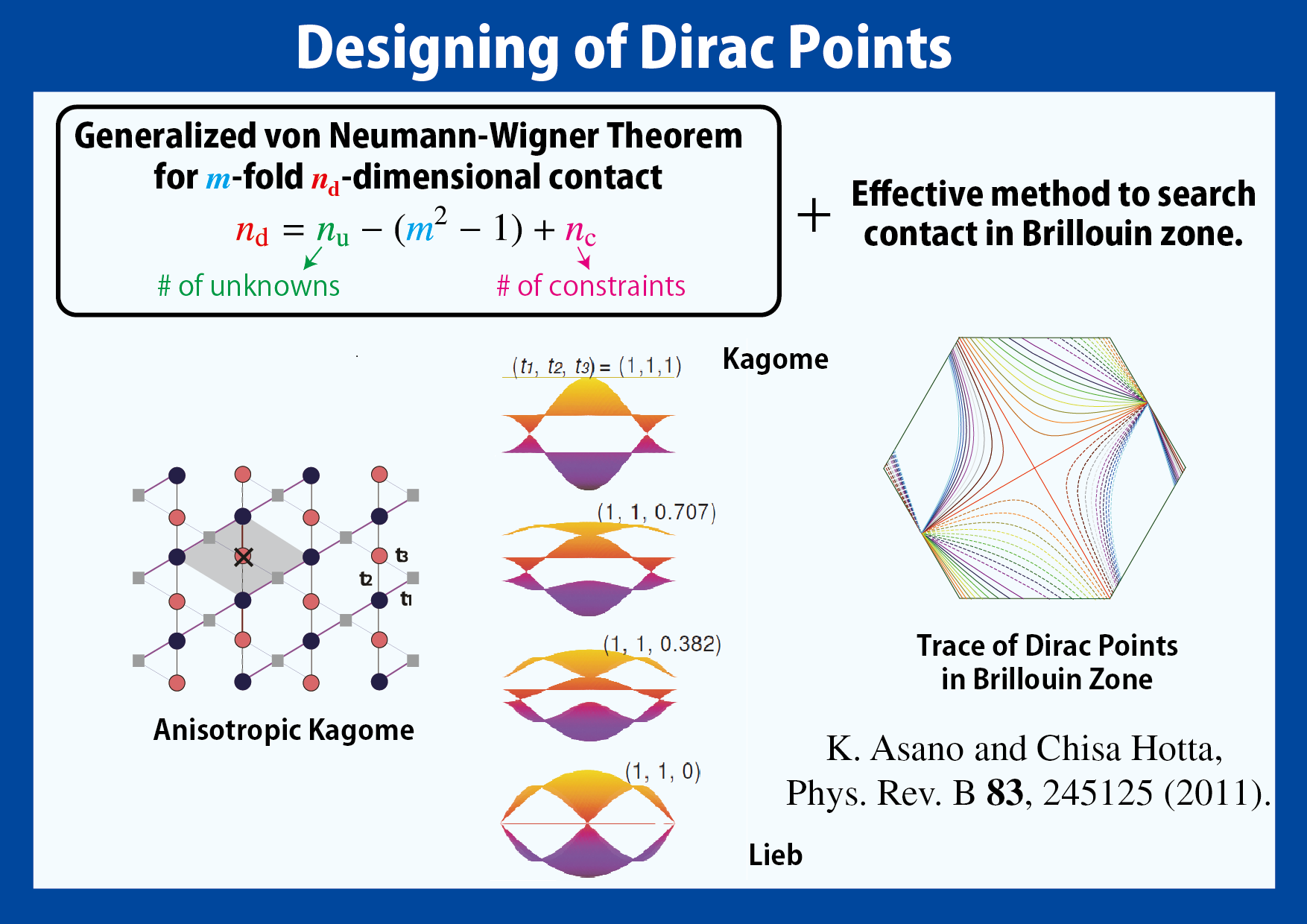
以上の事実を踏まえて,この研究では,(1) Dirac 点が現れる格子系の候補を(具体的に固有方程式を解くことなしに)選別する方法,(2) Dirac
点の位置を効率よく特定する手法の二点について考えました.ここで重要なのは「実現可能」なバンドの縮退です.理論家が設計した系を,実験的に厳密に再現することは不可能なので,バンドパラメータを精密に調節しないと実現しない縮退は意味がないからです.我々は,m重縮退点が,Brillouin
ゾーン内で nd 次元の k
点の集合を成す状況が「実現可能」となる条件を,一般化された von-Neumann-Wigner 条件として表しました.
同時に,バンド縮退が起こる k 点の位置を効率良く探索する手法も開発しました.これは m×m 行列形式の Green 関数(縮約されたm×m 有効ハミルトニアン)に着目し,縮退を持つエネルギー固有値のみを選択的に求めるものです.この方法は大変有用で,簡単な格子模型であれば,この手法を使って解析的にDirac 点の位置を特定したり,縮退点が現れるバンドパラメータの範囲を特定することも可能です.
同時に,バンド縮退が起こる k 点の位置を効率良く探索する手法も開発しました.これは m×m 行列形式の Green 関数(縮約されたm×m 有効ハミルトニアン)に着目し,縮退を持つエネルギー固有値のみを選択的に求めるものです.この方法は大変有用で,簡単な格子模型であれば,この手法を使って解析的にDirac 点の位置を特定したり,縮退点が現れるバンドパラメータの範囲を特定することも可能です.
- Kenichi Asano and Chisa Hotta: Physical Review B 83, 245125 (2011).
密度がアンバランスな電子正孔二層系における量子凝縮相
 タイプIIと呼ばれる量子井戸構造や,厚み方向に非対称な形状を持つ量子井戸を用いると,電子と正孔を空間的に離した二次元面に閉じ込めることが可能です.この系では電子と正孔が対消滅する時間スケールが非常に長いので,電子正孔系が極低温になるまで待つことができます.実際,この原理を利用して励起子の
Bose-Einstein 凝縮を実現したという実験の報告もあります.
タイプIIと呼ばれる量子井戸構造や,厚み方向に非対称な形状を持つ量子井戸を用いると,電子と正孔を空間的に離した二次元面に閉じ込めることが可能です.この系では電子と正孔が対消滅する時間スケールが非常に長いので,電子正孔系が極低温になるまで待つことができます.実際,この原理を利用して励起子の
Bose-Einstein 凝縮を実現したという実験の報告もあります.
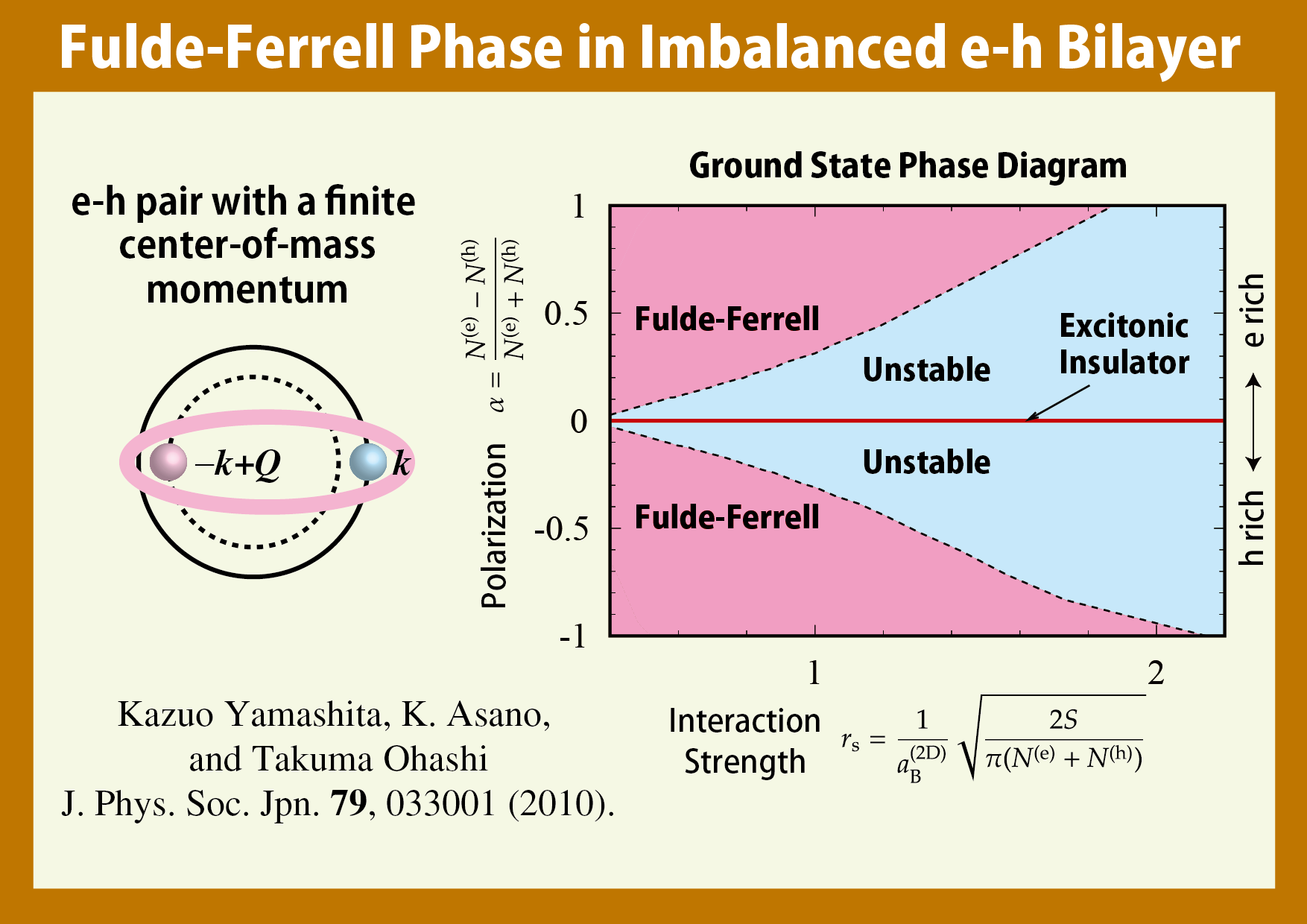
我々はこのような電子正孔二層系で,電子と正孔が異なる密度を持っていたときに,絶対零度でどのような凝縮相が現れるのかという問題について考察しました.我々の研究以前は,電子と正孔が重心運動がゼロの対を作って凝縮し,対を作れなかったキャリアーは単純に
Fermi 縮退した Sarma 相が現れると考えられていました.しかし,実際には重心運動量がゼロでない電子正孔対が凝縮する Flude-Ferrell
相の領域が大きく広がり,相互作用が弱い領域では Sarma 相はまったく現れないことが示されました.
- Kazuo Yamashita, Kenichi Asano and Takuma Ohashi: Journal of the Physical Society of Japan 79, 033001 (2010).